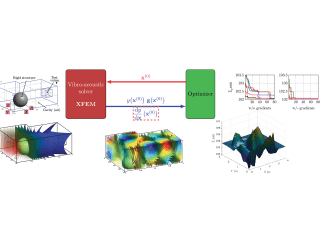
Vibro-acoustics problems solved using XFEM and parametric optimisation based on Gaussian Process
Using global parametric optimisation methodologies for coupled problems such as vibro-acoustics generally requires significant computational costs. Indeed, conventional optimisers generally require a large number of phy- sical problem resolutions in order to efficiently locate the optimum. In order to move towards a viable approach for this type of problem, several ingredients are proposed in the context of this work. These are (1) recent developments of a vibro-acoustic solver based on the extended finite element method (XFEM) [1] capable of providing responses and gradients efficiently and (2) the use of Bayesian Optimisation [2] based on a surrogate model enriched by the gradients of the objective function.
The used solver allows in particular the consideration of thin structures immersed in the fluid cavity. In order to avoid as much as possible the remeshing phases, the potential difficulties of obtaining compatible meshes between the fluid domain and the structure as well as the reconstruction of the finite element operators, the approach used allows the integration of any structures in the fluid domain without considering compatible meshes or remeshing steps. The discontinuity of the pressure field related to the presence of the wall is then taken into account by using an extended finite element method based on enriched shape functions (XFEM) [3, 1]. The fluid-structure coupling is then carried out via the new degrees of freedom introduced by the enrichment. The use of a description of the structure through level-sets together with the XFEM approach allows, not only, the consideration of complex geometry of the structure, but also the calculation of parametric gradients via a direct approach. Some examples of the implementation of the fluid-structure coupling will be presented. The gradient calculation approach will also be presented on simple cases integrating rigid structures.
The Bayesian Optimisation (BO) strategy [2] implemented is based on an iterative process of enrichment of a surrogate model (metamodel) providing an approximation of the true function. Gaussian Process surrogate models [4, 5] are built on the basis of responses and gradients of the objective function calculated by the physical solver for a reduced number of parameter sets. In a second step, a process of enrichment of the surrogate model is implemented using an expected improvement criterion. This approach allows the minimum to be obtained in a limited number of evaluations of the costly actual objective function. The inclusion of parametric gradients within the surrogate model allows, among other things, a significant increase in the quality of approximation, especially in the case of objective functions with strong multimodality. The optimisation approach will be presented and implemented on acoustic and vibro-acoustic examples. The contribution of gradients within the optimisation approach will be discussed in particular.
Joint work with Pr. Antoine LEGAY (LMSSC, Cnam).
References
[1] Antoine Legay. An extended finite element method approach for structural-acoustic problems involving immersed structures at arbitrary positions. International Journal for Numerical Methods in Engineering, 93(4) :376–399, 2013.
[2] Donald R. Jones, Matthias Schonlau, and William J. Welch. Efficient global optimization of expensive black- box functions. Journal of Global optimization, 13(4) :455–492, 1998.
[3] Nicolas Moe¨s, John Dolbow, and Ted Belytschko. A finite element method for crack growth without reme- shing. International Journal for Numerical Methods in Engineering, 46(1) :131–150, 1999.
[4] Carl Edward Rasmussen and Christopher K. I. Williams. Gaussian Processes for Machine Learning. Adaptive Computation and Machine Learning. The MIT Press, Cambridge, MA, USA, 01 2006.
[5] Luc Laurent, Rodolphe Le Riche, Bruno Soulier, and Pierre-Alain Boucard. An overview of gradient-enhanced metamodels with applications. Archives of Computational Methods in Engineering, 26(1) :61–106, 1 2019.