Séminaire : Luc LAURENT

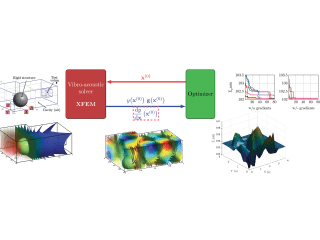
La mise en œuvre de méthodologies d’optimisation paramétrique globale pour les problèmes couplés tel que ceux de la vibro-acoustique nécessitent généralement des coûts de calcul important. En effet, les optimiseurs conventionnels requièrent généralement un grand nombre de résolutions du problème physique afin de localiser efficacement l’optimum. Afin de tendre vers une approche viable pour ce type de problèmes, plusieurs ingrédients sont proposés dans le cadre de ce travail. Il s’agit (1) de développements récents d’un solveur vibro-acoustique basé sur la méthode des éléments finis étendus [1] capable de fournir des réponses et gradients de manière efficace et (2) de l’emploi de l’Optimisation Bayésienne [2] s’appuyant sur un modèle de substitution enrichi par les gradients de la fonction objectif.
Le solveur employé permet en particulier la prise en compte de structures minces immergées dans la cavité fluide. Dans le but d’éviter au maximum les phases de remaillage, les potentielles difficultés d’obtention de maillages compatibles entre le domaine fluide et la structure ainsi que la reconstruction des opérateurs éléments finis, l’approche employée autorise l’intégration de structures quelconques dans le domaine fluide sans considérer de maillages compatibles ni d’étape de remaillage. La discontinuité du champ de pression liée à la présence de la paroi est alors prise en compte par l’emploi d’une méthode éléments finis étendus basée sur des fonctions de forme enrichies (XFEM) [3, 1]. Le couplage fluide-structure est ensuite réalisé via les nouveaux degrés de liberté liés à l’enrichissement. L’emploi d’une description de la structure par le biais de level-sets conjointement à l’approche XFEM permet, non seulement, la prise en compte de géométrie complexe de la structure, mais permet également le calcul de gradients paramétriques via une approche directe. Quelques exemples de mise en œuvre du couplage fluide-structure seront présentés. L’approche de calcul des gradients sera également présentée sur des cas simples intégrant des structures rigides.
La stratégie d’Optimisation Bayésienne [2] mise œuvre s’appuye sur un processus itératif d’enrichissement d’un modèle de substitution (métamodèle) fournissant une approximation de la véritable fonction. De type Processus Gaussien [4, 5], les modèles de substitution employés sont construit sur la base de réponses et gradients de la fonction objectif calculé par le solveur physique pour un nombre réduit de jeux de paramètres. Dans un second temps, un processus d’enrichissement du modèle de substitution est mis en œuvre via l’emploi d’un critère de type amélioration espérée. Cette démarche permet l’obtention du minimum en un nombre limité d’évaluations de la véritable fonction objectif couteuse. La prise en compte des gradients paramétriques au sein du modèle de substitution permet, entre autres, à nombre de jeux de paramètres fixés d’accroitre significativement la qualité d’approximation en particulier dans le cas de fonctions objectif présentant une forte multimodalité. La démarche d’optimisation sera présentée et mise en œuvre sur des exemples acoustique et vibro-acoustique. L’apport des gradients au sein de la démarche d’optimisation sera en particulier discuté.
Travail conjoint avec Pr. Antoine LEGAY (LMSSC, Cnam).

Références

[1]    Antoine Legay. An extended finite element method approach for structural-acoustic problems involving immersed structures at arbitrary positions. International Journal for Numerical Methods in Engineering, 93(4) :376–399, 2013.
[2]    Donald R. Jones, Matthias Schonlau, and William J. Welch. Efficient global optimization of expensive black- box functions. Journal of Global optimization, 13(4) :455–492, 1998.
[3]    Nicolas Moe¨s, John Dolbow, and Ted Belytschko. A finite element method for crack growth without reme- shing. International Journal for Numerical Methods in Engineering, 46(1) :131–150, 1999.
[4]    Carl Edward Rasmussen and Christopher K. I. Williams. Gaussian Processes for Machine Learning. Adaptive Computation and Machine Learning. The MIT Press, Cambridge, MA, USA, 01 2006.
[5]    Luc Laurent, Rodolphe Le Riche, Bruno Soulier, and Pierre-Alain Boucard. An overview of gradient-enhanced metamodels with applications. Archives of Computational Methods in Engineering, 26(1) :61–106, 1 2019.