From
Timetable
Place Amphithéâtre Dorothy Hodgkin (bâtiment Ouest, 0I10), École Normale Supérieure Paris-Saclay, 4 Avenue des Sciences, 91190 Gif-
Réduction de modèle pour les problèmes non linéaires de structures avec interfaces de contact multiples
Malgré les progrès continus en mécanique du contact, la simulation d’une structure complexe avec de multiples interfaces de contact frottant nécessite toujours un coût de calcul élevé en raison de multiples sources de nonlinéarité : évolution du statut de contact et de frottement, dissipation par frottement, grands glissements et grandes déformations.
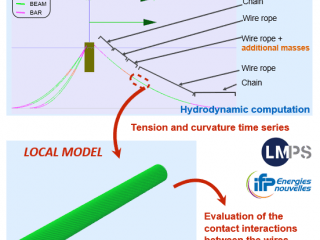
Cela peut induire des limitations pour les applications industrielles impliquant des matériaux architecturés tels que les câbles spiralés comportant de nombreux fils en contact, souvent utilisés en ingénierie offshore, ce qui a motivé ce travail. Parmi les stratégies alternatives pour réduire les coûts de calcul, une solution attractive consiste à projeter le problème d’ordre complet sur une base d’ordre réduit du problème original par diverses techniques de réduction de modèle. Cependant, leur application aux problèmes de frottement reste une question ouverte, en particulier pour les cas impliquant de grandes propagations de fronts de glissement/adhérence.
La stratégie proposée repose sur le solveur nonlinéaire LATIN (LArge Time INcrement) combiné à une réduction de modèle basée sur la Proper Generalized Decomposition (PGD). La LATIN présente un traitement robuste des conditions de contact et conduit naturellement à une méthode mixte de décomposition de domaine.
Par ailleurs, la formulation spatio-temporelle globale de la méthode permet d’utiliser la réduction de modèle basée sur la PGD pendant les calculs, en créant et en enrichissant à la volée des bases réduites par sous-domaine afin de mieux suivre les fronts de glissement et les phénomènes de propagation.
L’introduction d’une stratégie multiéchelle dans le cadre de la LATIN est cohérente avec la physique des problèmes de contact dans lesquels des phénomènes de longueurs d’onde différentes interagissent : les solutions locales aux interfaces de
contact présentent des effets de gradient élevés avec une longueur d’onde courte par rapport à la longueur caractéristique de la structure. En tirant parti de ce fait, le problème grossier de la stratégie permet de capturer efficacement le comportement du problème à l’échelle de la structure, en se focalisant ensuite sur la capture des variations de contact locales aux interfaces de contact.
Le point crucial de la thèse est que le modèle réduit doit représenter très fidèlement les informations critiques situées sur les interfaces de frottement entre les fils, qui sont cruciales pour l’évaluation de leur durée de vie en fatigue. L’objectif est de rechercher à maximiser les performances de réduction de modèle et la vitesse de convergence, tout en garantissant une évaluation précise des quantités d’interface. A cette fin, les critères
de convergence pour la méthode de résolution nonlinéaire doivent assurer une bonne convergence pour les quantités de contact locales.
De plus, une mise à jour appropriée des directions de recherche de la LATIN permet d’augmenter de manière significative la vitesse de convergence. Enfin, pour les problèmes très irréguliers tels que les problèmes de contact frottant, le contrôle de la qualité et de la taille des bases PGD construites progressivement le long des itérations de la LATIN est crucial pour l’efficacité de la méthode.
Le jury sera composé des membres suivants :
- Anthony GRAVOUIL, Professeur des Universités, INSA Lyon - Rapporteur & Examinateur.
- Pierre KERFRIDEN, Professeur des Universités, Mines Paris - PSL - Rapporteur & Examinateur.
- Florence BERTAILS-DESCOUBES, Directrice de Recherche, INRIA Grenoble Rhône-Alpes - Examinatrice.
-
Pierre GOSSELET, Directeur de Recherche, Université de Lille - Examinateur.
-
Daniel RIXEN, Professeur des Universités, TU München - Examinateur.