Mécanique de l’endommagement non-local avec interactions évolutives pour la modélisation des matériaux quasi-fragiles : endommagement anisotrope et approche Eikonale à gradient implicite
La prévision de la nucléation et de la propagation des fissures est essentielle pour décrire la réponse des structures dans des conditions de chargement complexes. On
observe l’apparition de microfissures diffuses avant la formation d’une macro fissure. Dans le cas de matériaux quasi fragiles, on observe un comportement adoucissant lié à une perte progressive de rigidité. D’un point de vue thermodynamique, ce comportement peut être décrit de manière continue par une variable d’état d’endommagement. Cependant, les modèles
d’endommagement locaux conduisent inévitablement à un problème aux valeurs limites mal posé. Dans un contexte d’éléments finis, les résultats numériques dépendent donc du maillage.
Les modèles d’endommagement non locaux permettent d’obtenir des résultats indépendants du maillage en introduisant des interactions de voisinage par le biais d’une longueur interne. Les approches non locales classiques considèrent des interactions isotropes et constantes, ce qui ne permet pas de reproduire correctement l’ensemble du processus de dégradation. Des approches prenant en compte des interactions évolutives existent et peuvent mieux décrire le comportement de la fissuration. Cette thèse vise à fournir des aspects théoriques et numériques pour le développement de modèles d’endommagement à gradient implicite avec interactions évolutives. Tout d’abord, les modèles non-locaux sont étudiés et comparés en analysant les effets de bord et la diffusion de l’endommagement dans un essai d’écaillage unidimensionnel en dynamique explicite.
L’approche non-locale Eikonale est étudiée, où les interactions évolutives sont considérées par le biais d’une métrique riemannienne dépendante de l’endommagement. La version
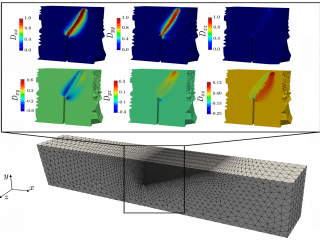
avec gradient de ce modèle (ENLG) est ensuite dérivée d’un cadre micromorphe basé sur la géométrie différentielle, conduisant à une expression de dissipation respectant au second principe de la thermodynamique. Une formulation variationnelle simplifiée est développée pour évaluer les capacités du modèle dans des simulations numériques quasi statiques bidimensionnelles avec endommagement isotrope. Enfin, la régularisation ENLG est couplée à un modèle d’endommagement anisotrope prenant en compte un tenseur d’endommagement de second ordre. L’anisotropie
induite est naturellement prise en compte dans le comportement et dans les interactions évolutives. Des simulations en deux et trois dimensions sont étudiées et comparées aux résultats expérimentaux existants dans la littérature, tout en soulignant les aspects numériques associés. Une analyse détaillée décrit les avantages de la prise en compte de l’endommagement anisotrope et des interactions anisotropes dépendantes de l’endommagement.
Le jury sera composé des membres suivants :
- Djimédo KONDO, Professeur des Universités, Sorbonne Université, Examinateur.
- Gilles PIJAUDIER-CABOT, Professeur des Universités, Université de Pau et des Pays de l'Adour, Rapporteur & Examinateur.
- Nicolas MOËS, Professeur des Universités, École Centrale de Nantes, Rapporteur & Examinateur.
- Bert SLUYS, Professeur, TU Delft, Examinateur.
-
Rodrigue DESMORAT, Professeur des Universités, ENS Paris-Saclay, Examinateur.
-
Domenico GENTILE, Professeur, Università degli Studi del Molise, Examinateur.