Séminaire : Virginie Ehrlacher

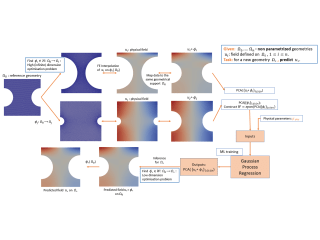
L'objectif de cet exposé est de présenter des premiers résultats récents obtenus sur une nouvelle méthode de morphing pour construire des modèles réduits. L'objectif de ce travail in fine est d'accélérer le temps de simulation de problèmes de mécanique où la géométrie du domaine occupé par le solide d'intérêt est variable, mais ne peut pas être décrite par le biais d'un petit nombre de paramètres. La méthode numérique repose sur plusieurs étapes. Dans un premier temps, en supposant que l'on dispose d'une base de données de géométries et de champs d'intérêt (déplacements, contraintes), on cherche à calculer un difféomorphisme entre chaque géométrie de la base de données et une géométrie de référence. Ces difféomorphismes sont ensuite optimisés de sortie à pouvoir compresser au mieux les champs d'intérêt déformés via ces difféomorphismes par le biais d'une décomposition POD. Ces deux étapes constituent l'étape "offline" de la méthode. Nous présenterons ensuite une méthode online efficace pour le calcul rapide des champs d'intérêt lié à une nouvelle géométrie, reposant sur le calcul efficace d'un difféomorphisme optimisé entre la nouvelle géométrie et la géométrie de référence. Nous illustrerons le comportement de la méthode sur plusieurs cas tests d'intérêt. Ce travail est issu d'une collaboration avec Felipe Bordeu, Fabien Casenave Alexandre Ern et Abbas Kabalan.