Séminaire : Jean-Michel Bergheau

La prédiction des conséquences métallurgiques et mécaniques induites par les procédés de fabrication thermo-mécaniques, requiert des simulations numériques thermo-élastoplastiques ou viscoplastiques fortement non-linéaires. Alors que ces simulations ont longtemps concerné des géométries relativement simples, localisées dans un voisinage des zones affectées, les industriels souhaitent travailler aujourd’hui sur les géométries réelles généralement complexes et tridimensionnelles.

Mais la prise en compte d’un comportement élastoplastique pour des matériaux obéissant au critère de von Mises peut induire des phénomènes de blocage, liés à l’incompressibilité plastique, nécessitant l’utilisation d’éléments finis particuliers (intégration réduite, formulations mixtes…). La nécessité d’utiliser ces éléments conduit alors à des surcoûts d’études très significatifs liés notamment à la phase de maillage.

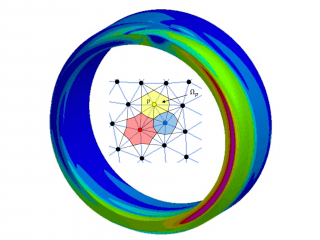
Dans l’objectif principal d’aboutir à une méthode numérique offrant le meilleur compromis possible entre la durée d’étude (incluant les phases de maillage, de résolution et d’analyse des résultats) et la précision des résultats, nous proposons une nouvelle méthode des éléments finis reposant sur une intégration nodale et des maillages en tétraèdres (NIFEM : Nodal-Integration-based Finite Element Method). L’existence d’outils performants de maillage automatique en tétraèdres confère en effet à ce type d’élément fini un avantage économique indiscutable. D’autre part, le choix des nœuds comme points d’intégration semble optimal pour ce qui concerne le phénomène de blocage volumique.

Le choix des nœuds comme points d’intégration n’est pas nouveau. On retrouve cette idée notamment dans Dohrman et al [1], Krysl et Zhu [2], dans la méthode NS-FEM (Node-based Smoothed Finite Element Method) [3] ou dans les méthodes sans maillage [4]. Ces méthodes se distinguent principalement par la façon de calculer les déformations nodales. Nous montrons que dans le cas d’un maillage quelconque en tétraèdres, certaines de ces méthodes sont en fait équivalentes [5]. Le calcul des contraintes sur les surfaces extérieures ou à l’interface de deux matériaux, très imparfait avec la méthode originale, est ensuite amélioré grâce à un algorithme d’intégration spécifique des équations constitutives du matériau en ces points [6].

Un module de thermo-métallurgie, compatible avec le module de calcul mécanique de la NIFEM, est développé. L’équation de la chaleur est formulée en enthalpie [7] pour reproduire les phénomènes de recalescence. Toutes les variables d’état (température, proportions de phases…) sont calculées aux nœuds.

Enfin, comme de nombreux procédés thermomécaniques mettent en jeu des sollicitations mobiles par rapport à la matière (soudage, laminage…), un algorithme original de calcul des états mécaniques quasi-stationnaires pour ces problèmes est proposé.

 

[1].    Dohrmann CR, Heinstein MW, Jung J, Key SW, Witkowski WR (2000) Node-based uniform strain elements for three-node triangular and four-node tetrahedral meshes. Int J Numer Methods Eng, 47:1549–1568
[2].    Krysl P., Zhu B., Locking-free continuum displacement finite elements with noda lintegration, Int. J. for Numer. Meth. In Eng., 2008,; 76: 1020-1043.
[3].    H. Yang, X. Y. Cui, S. Li, Y. H. Bie (2018), A stable node-based smoothed finite element method for metal, Computational Mechanics, https://doi.org/10.1007/s00466-018-1641-2
[4].    Jiun-Shyan Chen, Cheng-tang Wu, Sangpil Yoon, and Yang You. A stabilized conforming nodal integration for Galerkin mesh-free methods. Int. J. for Numer. Meth. In Eng., 2001, 50, 435-466.
[5].    Jia, Y., Bergheau, J.-M., Leblond, J.-B., Roux, J.-C., Bouchaoui, R., Gallée, S., & Brosse, A. (2020). A new nodal-integration-based finite element method for the numerical simulation of welding processes. Metals, 10(10), 1-18. doi:10.3390/met10101386
[6].    Jia, Y., Leblond, J.-B., Bergheau, J.-M. (2022). Exact satisfaction of boundary and interface conditions in nodal-integration-based finite element methods. Comptes Rendus Mécanique 350 (G1), 57-83
[7].    Leblond, J.-B, Bergheau, J.-M., Lacroix, R., & Huin, D. (2017). Implementation and application of some nonlinear models of diffusion/reaction in solids. Finite Elements in Analysis and Design, 132, 8-26. doi:10.1016/j.finel.2017.04.004