Séminaire : Cédric Bellis

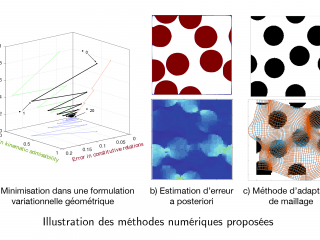
The homogenization of periodic elastic composites can be addressed through the reformulation of the local equations of the mechanical problem into energetic variational principle. We review such principles and describe a computational, FFT-based, approach that has shown effective on a variety of problems. Building on these tools, we propose some novel geometric variational formulations of the problem, which feature functionals that aim at measuring the discrepancy of arbitrary test fields to the kinematic, static or material admissibility conditions of the problem. By relaxing the corresponding local equations, this formulation aims in particular at laying the groundwork for the homogenization of composites whose constitutive properties are only partially known or uncertain, or to make use of data-driven approaches.
In addition, we will discuss some strategies for constructing a posteriori error estimators for FFT-based spectral methods and, such methods generally lack precision in the presence of discontinuities or singularities, we will propose a numerical method for improving their performance.